Evaluation Implications of Sub-Optimum Pricing

Part of Toolkit for the Economic Evaluation of World Bank Transport Projects

(Institute for Transport Studies, University of Leeds, 2003)

General principles:

· Investment should always be appraised on the basis of a specified pricing policy.

· Demand forecasts should be consistent with the pricing policy specified, and the economic evaluation should be based on these demand forecasts.

Transport pricing includes:

- infrastructure charges, such as road tolls, rail track access charges, airport landing fees and port dues;

- fares and tariffs to service users, such as rail and bus passenger fares, air fares, ferry fares, and tariffs on all modes for freight service.

Pricing is sometimes a source of difficulties in project appraisal, due to:

i) the inter-dependence of pricing and economic benefits, and

ii) the uncertainty which sometimes surrounds pricing policy, at the stage when the economic appraisal is carried out.

This note will deal extensively with point (i), and will indicate how point (ii) can be addressed as part of the risk and uncertainty analysis (see Note Risk and Uncertainty Analysis [Link]. Point (ii) highlights a wider process issue in project development: that the design and even the appraisal of major projects are sometimes completed before what are sometimes regarded as ‘tactical’ pricing decisions such as toll or tariff-setting. Yet, as this Note shows, the economic benefits of projects are closely inter-related with the price regime. It makes no sense to appraise an investment without considering pricing aspects. (It also makes no sense to develop a pricing policy without considering the investment dimension – however that is not the main focus of this Toolkit).

The note focuses on three specific ways in which sub-optimal pricing can impact on project benefits:

1. through congestion and overcrowding (Section 1);

2. through overpricing and loss of user benefits (Section 2); and

3. through financial deficits which have implications for the rest of the economy (Section 3).

Sections (1-3) of the Note seek to give practical advice on each situation, including how to approach the economic analysis of the situation, and the key implications for project appraisal.

If pricing policy is not known with certainty at the time of the appraisal, then alternative pricing policies must form part of the risk and uncertainty analysis. This is covered in Section 4. Conclusions are given in Section 5.

1 Congestion and overcrowding

A common problem affecting transport infrastructure and services is that they are congestible. In the case of infrastructure – roads, railways, airports and so on – the obvious symptoms of congestion include queuing and an increase in overall journey times. In the case of passenger transport services, the obvious symptoms also include overcrowding where overcrowding is allowed, typically on trains and buses. In addition to these observable symptoms, there is also the hidden symptom of suppressed demand – those potential customers who choose not to use the facility at all because of the congested conditions which exist.

In economic analysis, congestion is represented as part of the supply function. This is done by expressing supply in terms of generalised cost rather than simply money cost (see Framework [Link]). As demand for a particular transport link increases, the level of service provided by the link deteriorates – for example in terms of journey time – and so the generalised cost faced by users rises (Figure 1).

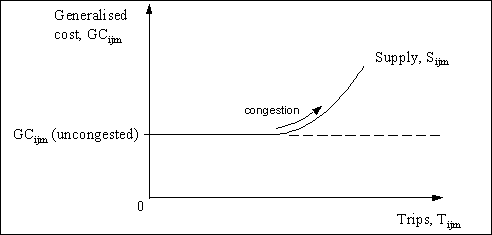
FIGURe 1: CONGESTION AS A FEATURE OF transport SUPPLY CONDITIONs

Transport infrastructure investment projects usually aim to increase the capacity or quality of the infrastructure, leading to benefits for new and existing users. However, these benefits can be eroded by congestion. Figure 2 shows how this can occur.

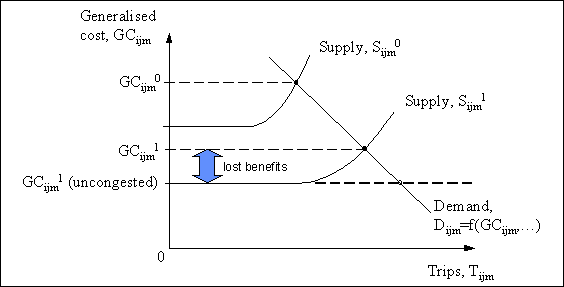
FIGURe 2: EROsion of project benefits by CONGESTION

The investment shifts the supply function outwards and downwards: more trips are possible at any given price (generalised cost), and the price (generalised cost) associated with each level of traffic is reduced. In short, the new facility provides for more trips at a lower generalised cost.

Note, however, that in this Figure the new supply function, S_ijm¹, cuts the demand curve at a point where the demand curve is upward-sloping. Congestion has already set in.

Urban Motorway Example

Consider, for example, a project for a new urban motorway. The aim is to facilitate faster, cheaper and safer transport to and from key locations within the city. The motorway is designed to have a capacity of 5400 vehicles per hour in each direction. However, the speed-flow relationships for this type of road mean that above 3500 vehicles per hour, traffic speeds start to slow down significantly – and therefore journey times, and generalised costs, increase.

When the project is designed, the design team calls on a demand modelling specialist to provide forecasts of peak and off-peak traffic on the new motorway (see the Framework [Link] and Note Demand Forecasting Errors [Link]. Figure 3 illustrates, for the peak hour, both the demand function – showing the predicted demand for the road at each level of generalised cost – and the supply function – showing what will be the generalised cost of using the road at each level of traffic flow.

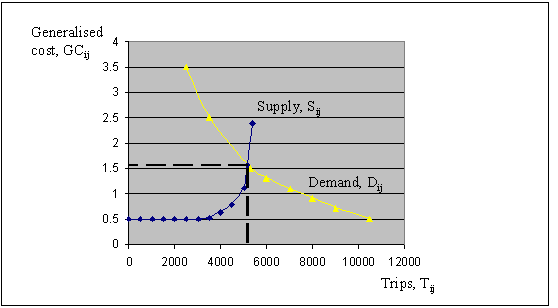
FIGURE 3: NUMERICAL EXAMPLE – PEAK HOUR PRICING ON A NEW URBAN MOTORWAY

In equilibrium, when the system is left to settle down, the expected outcome is:

Peak hour conditions (0700-0800 hours)

- traffic speed, 32 km/h (average)

- generalised cost, $1.56

- traffic flow, 5200 vph

The analysis illustrated in Figure 3 shows how congestion can erode the benefits of a new investment project. The motorway had a design speed of 100 km/h, yet its performance in the peak hour was only 32 km/h on average.

Pricing to protect project benefits

Pricing can be used to prevent the excessive erosion of project benefits by congestion, as follows.

A key feature of congestion is that it involves a user-on-user externality. In other words, as an extra vehicle enters the congested section, it not only slows down the flow for itself, but for other users as well. This effect on other users is called the Marginal External Cost (MEC). As a result, the Marginal Social Cost of travel (MSC) is pushed up above the Marginal Private Cost of travel (MPC):

MSC = MPC + MEC

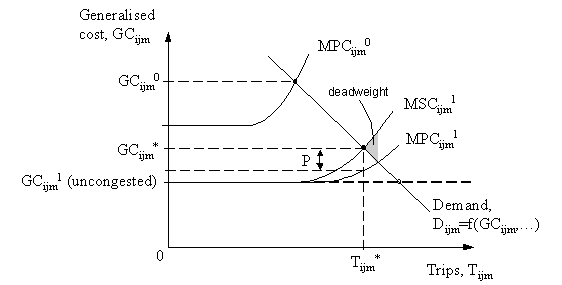
FIGURe 4: Pricing to protect project benefits

The literature on efficient transport pricing (see Walters (1968) [[1]], Newberry (1990) [[2]], Hau (1992a) [[3]] and Hau (1992b) [[4]] finds that by levying a congestion charge equal to P, a more efficient outcome is achieved. P is the difference between the Marginal Social Cost and the Marginal Private Cost at the optimum (T*,GC*). An economic model will usually be required to estimate P. See Hau (1992a and 1992b) [3] [4] for further information.

An alternative approach – practised in Singapore – is to choose a level of service (e.g. a specified average speed) for peak traffic, and then to vary the toll until that level of service is achieved.

As can be seen in Figure 4, the congestion charge deters some users from travelling. However, at the same time, a revenue is generated from the tolls paid, and the ‘deadweight efficiency loss’, which would have occured without congestion charging, is eliminated.

In the urban motorway example above, we can see the effect of charging a toll using the economic analysis we developed earlier. A $1 toll has the effect of increasing the peak hour traffic speed to 60 km/h, whilst a $2 km/h toll leads to a peak hour traffic speed of 95 km/h. The user benefits of these changes are calculated in the usual way described in Framework [Link], using the Rule-of-a-Half. The revenue which is generated by the toll can be calculated straightforwardly: it is P*ΔT¹_ijm where P is the toll and ΔT_ijm is the number of trips remaining on the road when the toll is in place.

TABLE 1: NUMERICAL EXAMPLE – PEAK HOUR PRICING ON A NEW URBAN MOTORWAY

Toll	per hour
Toll	Demand, trips	User benefits, $	Revenue, $	Net Benefit, $
$0	5200	12 714	0	12 714
$1	4600	11 538	4 600	16 138
$2	3500	8 538	7 000	15 538

Note: (i) Net Benefits = User benefits + Revenue; (ii) the benefits quoted are the benefits of the motorway compared with the ‘no motorway’ scenario, under alternative tolling assumptions.

It can be seen from Table 1 that, in terms of overall Net Present Value, a $1 peak hour toll gives the best economic return. A $2 toll will increase the revenue generated but that gain would be more than offset by the loss of user benefits, since an extra 1100 users are priced off the road by the higher toll.

Note that with further analysis the toll could be optimised for efficiency, to $1 +/– a certain number of cents. It is worth bearing in mind, however, that there are higher transactions costs associated with more complicated tolls; a $1 toll has the advantage of being simple for users to remember and relatively easy to collect in cash.

Note also that at the optimal toll, there is still a certain amount of congestion on the road. This is a general result for road pricing: the optimal level of congestion is likely to be positive, not zero.

Issues to consider

Having presented the central part of the analysis, it is worth highlighting a number of issues around pricing which often arise in World Bank-funded projects:

i) There may be equity implications for citizens with a low income and low ability to pay. These are the citizens most likely to be priced off the new motorway by the toll, since they are the most sensitive to the money component of the generalised cost. Furthermore, these citizens may also stand to lose the most from the motorway project, if they are especially reliant on any local land and resources which are displaced by the motorway.

Two approaches may be helpful in addressing such issues. Firstly, the overall equity impact will be determined by the way in which the toll revenue is used. If part of the revenue is channelled to low income citizens, for example by reducing labour taxes on the poor, then the distributional effects may be mitigated to some extent. Secondly, a more specific intervention would be to seek to address the mobility needs of low income citizens by providing public transport services using the new motorway. Financing for this – if required – could be drawn from the toll revenues, although it should be borne in mind that The World Bank itself does not provide funding for public transport subsidy.

For further discussion of projects which actively benefit the poor, see the Note Distribution of Benefits and Impacts on Poor People [Link].

ii) If there is a very large suppressed demand for the project, then very high prices may be required to avoid excessive congestion when the project opens. At the start of the project development process, it is worth thinking about whether this will become an issue and how to deal with it if it arises. One way of tackling this would be to consider increasing the scale of the investment, for example by adding to the number of lanes on the new urban motorway in the case discussed above. Any such increase would have to be justified in terms of its Net Present Value, nevertheless, if a high toll is required to manage demand, this provides a signal that additional investment may be justified.

2 OVERPrICING AND LOSS OF USER BENEFITS

By the conventional ‘law of demand’, increasing the price of a transport service usually leads to a reduction in the quantity demanded and a loss of consumer’s surplus. This situation is shown in Figure 5(a). From the consumer’s point of view, as long as there is no congestion or overcrowding, the lower the price, the better.

From a commercial transport operator’s point of view, revenue is the key variable. The relationship between price and revenue is not usually linear – instead, starting from a very low price and letting price gradually increase, revenue typically increases then falls back down again. In between, there is a point P^Rmax_ijm where revenue is maximised, as shown in Figure 5(b).

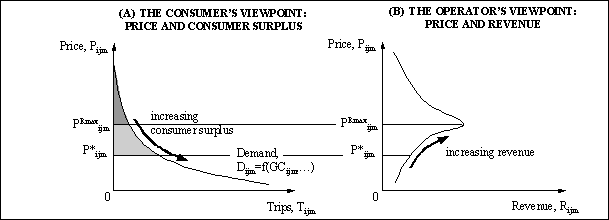
FIGURe 5: Pricing, CONSUMER SURPLUS AND REVENUE

In transport, operators often experience very large fixed costs – particularly in transport infrastructure – which means that in such cases P^Rmax is also the profit-maximising price. This makes the tension very clear, between the consumer’s objective (to minimise price) and the operator’s objective (to push the price up towards P^Rmax). Toll road operators and urban metro operators – to give just two examples – often find themselves in a position like this, where price is the critical variable in their profit function. The question is: how should this tension be resolved?

In transport markets where there is a substantial element of natural monopoly, such as a new tolled river crossing or an urban metro line, it is commonplace for a public authority to intervene to resolve this tension, rather than leave it to the market. The following analysis shows why, and outlines how an efficient price can be set.

Pricing policy to secure social objectives

Pricing can be viewed as a project in itself, with the overall goal being to maximise Net Present Value, as in any other transport project. There may also be a constraint: that the project is in some sense financially sustainable. For example, if the project is being contracted out through some form of Public Private Partnership, then the private sector partner will require a financial return commensurate with the costs and risks involved, and with the returns available elsewhere in the market. If the public sector is delivering the project, there may for example be a requirement that the project breaks even in financial terms, in addition to the goal of maximising net social benefit.

In Figure 4 above, we use P*_ijm to denote the lowest price at which the transport facility is financially sustainable.

Metro Example

Consider, for example, a new metro line. The city authority is responsible for the metro’s operating costs, which amount to $38,000 per day. Demand conditions are represented by the first two columns of Table 2. From this, it is clear that the lowest price at which the line is financially sustainable is $3 per passenger. The fourth and fifth columns show that User Benefits (calculated using the Rule-of-a-Half in the usual way), and indeed overall Net Benefits, would be maximised at a lower fare, however subject to the financial sustainability constraint, $3 is the optimum. A commercially-set fare of $4 would maximise revenues, however user benefits would be nearly 30% less.

TABLE 2: NUMERICAL EXAMPLE – METRO LINE

Fare, $	per day
Fare, $	Passengers	Revenue, $	User benefits, $	Net Benefit, $
0.5	17000	8500	79550	88050
1	16000	16000	71300	87300
1.5	15000	22500	63550	86050
2	14000	28000	56300	84300
3	12800	38400	42900	81300
4	11200	44800	30900	75700
5	8300	41500	21150	62650
6	6200	37200	13900	51100
7	3900	27300	8850	36150
8	2800	22400	5500	27900
9	1700	15300	3250	18550
10	1200	12000	1800	13800

Note: (i) Net Benefits = User benefits + Revenue; (ii) the benefits quoted are the benefits of the metro compared with the ‘no metro’ scenario, under alternative pricing assumptions.

By undertaking an economic analysis, we can identify cases of overpricing such as this. The results make it possible to identify an efficient price, subject to the financial constraints which exist for a particular project.

3 Creation of a deficit

Pricing also impacts on welfare through the producer’s surplus. If the price is pushed down below the minimum price at which costs are recovered (described above as the public sector’s financially sustainable price) or up above the maximum price at which costs are recovered (see Figure 5), a deficit is created which must be financed from other sources. A common assumption is that such deficits are financed by the government from additional general taxation, and if this is the approach, then the social cost of this deficit must be considered.

The social cost of a given deficit, will be equal to the deficit multiplied by the Marginal Cost of Public Funds (MCPF). The World Bank’s Handbook of Investment Operations (World Bank, 1998 [[5]]) explains how to calculate the MCPF for a particular application. Typically, values for the MCPF will be in the range 1.1 to 1.5, with 1.3 as a mean estimate.

In the metro line example given above, suppose that the daily operating costs of the metro are $50,000 instead of $38,000. In that case, a decifit of approximately $5,000 would arise in financial terms. The equivalent social cost would be $5,000*MCPF or approximately $5,000*1.3 = $6,500. This amount per day would need to be deducted from the overall NPV welfare calculation.

Note that the World Bank itself does not provide funding for deficits – therefore it is essential that the financial sustainability of the project be secured by other partners.

4 evaluation when there is Uncertainty over pricing policy

It is regrettably a common problem that a project has been designed without specifying the pricing policy, and that the appraisal must be delivered before the pricing policy is decided. This could apply to either of the examples used in this Note – a motorway or an urban metro – or to a wide range of other transport projects where pricing will affect the benefits – for example, a new airport or additional runway, or investment in a long distance rail freight network or inland waterway improvements.

Under these conditions, an approach consistent with the Note Risk and Uncertainty Analysis [Link] should be used, as follows:

- Step 1. Specify a range of possible pricing policy scenarios, including:

- a scenario which shows what the highest possible overall project benefits would be;

- a scenario (or scenarios) which would satisfy some other interest – for example, a revenue maximising scenario or a scenario where no tolls at all are imposed – but which would be relatively detrimental to the project’s net benefits;

- a ‘middle way’ scenario (or scenarios), aiming to maximise project benefits subject to any key constraints – including financial sustainability. More than one of these scenarios may be required in order to choose among different variants of pricing policy which are under discussion at the time the appraisal is undertaken, but on which no decision has been taken.

- Step 2. Use sensitivity analysis (see Note Risk and Uncertainty Analysis [Link]) to understand the effect on the Net Present Value of each scenario.

- Step 3. Test the impact on the NPV using quantitative risk analysis (Monte Carlo simulation) if you are able,

otherwise

report the results for each scenario separately, indicating which scenario or scenarios are believed to be the most likely, and if there are any scenarios with unacceptable NPVs (NPV<0) then what is the likelihood of these being the outcome.

5 CONCLUSIONS

The common theme which runs throughout the note is that for transport – as for any product:

- price influences demand, and

- in turn, demand influences producer revenues and user benefits.

It is most important that the demand model and demand forecasts for any project are based on price assumptions which are explicitly considered and agreed with the client as an appropriate scenario for testing, and that the pricing assumptions are stated explicitly in the appraisal.

The price assumptions affect the outcome of the appraisal in various ways:

- prices affect demand, user benefits and revenues on the facility being appraised, hence the overall Net Present Value of a project;

- prices on particular parts of the network can affect the performance of the rest of the system – if so, the appraisal needs to consider the effects of facility pricing at the network level, using the ijm network approach to appraisal set out in the Framework [Link];

- pricing can be used to reduce congestion and crowding to efficient levels (Section 1) – the effects on user benefits and revenues must be taken into account;

- economic analysis can be used to identify overpricing, including where commercial incentives come into play (Section 2) – efficient prices can be proposed which public authorities may wish to implement using contractual or legislative means;

- pricing strategies can sometimes lead to financial deficits (Section 3) – in economic analysis, such deficits need to be evaluated at their social cost, not at the money cost in which they are initially measured, using the Marginal Cost of Public Funds (MCPF).

Finally, when there is uncertainty over what pricing policy will be in place if the project is implemented, a form of Risk and Uncertainty Analysis is required (Section 4).