Figure 1. Sequence of traffic signal algorithms for clearance of peak hour queues.
CONTENTS
1. ABSTRACT
2. INTRODUCTION
3.1 Introduction
3.2 Traffic Signal Control in Congested Conditions
3.2.1 Introduction
3.2.2 Isolated Intersections
3.2.3 Linked Intersections
3.2.4 Urban Networks
3.3 Dynamic Change of Algorithm
3.3.1 Introduction
3.3.2 Gating and action at a distance
3.3.3 Congestion offsets
3.3.4 Congestion link facility - information from another link
3.4 Traffic Metering
3.4.1 Introduction
3.4.2 Local-scale measures
3.4.3 Area-wide measures
3.4.4 Real-World Applications
3.4.5 Disadvantages / Objections
3.5 Recovery from Severe Congestion
3.5.1 Introduction
3.5.2 Reduced Cycle Times
3.5.3 Sterilization of Spare Capacity
3.5.4 Driver Information Systems
3.6 UTC Operational Strategies
4. CONCLUSIONS
REFERENCES
BIBLIOGRAPHY
APPENDIX A - QUEUE MANAGEMENT PRINCIPLES
APPENDIX A1 Traffic Control in Oversaturated Street Networks
APPENDIX A2 Control of Congestion in Highly Congested Networks
APPENDIX A3 Strategies for the Management of Queues at Upstream Junctions
APPENDIX A4 Saturation control in the UTOPIA system
LIST OF TABLES
Table 1. List of Area Strategies: From DRIVE I Project V1015.
LIST OF FIGURES
Figure 1. Sequence of traffic signal algorithms for clearance of peak
hour queues.
Figure 2. Reverse progression signal offset.
Figure 3. Queue propagation between junctions.
Figure 4. The flared green progression along West-East cross-streets.
Figure 5. North-South arterial green times.
Figure A1. Horizontal and vertical queue evolution.
1. ABSTRACT
Traffic queues can be managed to make maximum use of existing facilities or they may be managed such that the input rate of traffic into a sensitive section of the road network is restricted. A range of queue management techniques has been used in saturated urban traffic conditions around the world. In most cases a combination of various techniques is used to form a strategy, or series of strategies, best suited to the road network configuration and local pattern of demand.
This paper reviews queue management strategies in the context of urban traffic congestion. Although attention is focused mainly on signal control measures, both static and dynamic, non-signal techniques are also mentioned. It is concluded that the formulation and use of each strategy will depend on whether the objective is to postpone, to handle or to recover from highly saturated conditions. In the context of a signal controlled urban corridor, a combination of reverse signal progression and metering would be required to form the most appropriate queue management strategy.
2. INTRODUCTION
Urban road networks in many of today's European cities exhibit high levels of traffic congestion during peak periods. Although congestion problems generally do not last more than an hour or so, there are examples of cities outside of Europe, such as Lagos and Bangkok, when traffic comes to a standstill for long periods of the day. It is generally accepted that the problem of urban traffic congestion has now reached such proportions that it is no longer merely a nuisance; it is becoming a threat to the economic viability of urban centres.
Longley (1968) identifies two forms of traffic congestion.
a) primary congestion:- caused by the development of queues at controlled junctions, and
b) secondary congestion:- arising from the blockage of other junctions by primary congested traffic.
Pignataro et al. (1978) provide more detailed definitions of various "congestion - related" traffic operations in controlled networks.
a) Uncongested Operations: refers to a situation where there is no significant queue formation. Traffic performance may range from very low demand per cycle to conditions where the demand is a substantial fraction of the capacity value. Short queues may occasionally form towards the upper end of this performance range, but do not last for any length of time.
b) Congested Operations: characterizes the entire range of operations which may be experienced when traffic demand approaches or exceeds the road and/or junction capacity. The realm of congested operations can be divided into two sub-categories: saturated and over-saturated operations.
i) Saturated Operations: is a term that describes that range of congestion wherein queues form, but their adverse effects on the traffic in terms of delay and/or stops are local.
ii) Oversaturated Operations: is characterized as a situation wherein a queue exists, and it has grown to the point where upstream traffic operations are adversely affected.
Longley (op cit) states that, when primary congestion is unavoidable, the control strategy should be aimed at avoiding or postponing the onset of secondary congestion. In fact, the range of objectives for control strategies is wider than this, and can be expressed as:
a) To prevent or postpone the attainment of saturated operations.
b) To handle saturation once it has been unavoidably attained.
c) To remedy or recover from the saturated conditions as expeditiously as possible.
Useful reviews of objectives and methods for tackling urban traffic congestion include; Pignataro et al. (1978), OECD (1981), ITE (1988), Huddart and Wright (1989) and Shepherd (1990).
3.1 Introduction
Pignataro et. al. (1978) classifies measures designed to tackle urban traffic congestion into:
a) Signal: minimal responsive policies
b) Signal: highly responsive policies
c) Nonsignal: other treatments in a signalized environment.
Huddart and Wright (ibid), in their review of ways of preventing catastrophic congestion, also classify treatments into three broad headings, these are:
a) Static Protection measures
b) Dynamic protection measures
c) Traffic input control.
In fact, all the various measures to combat congestion attempt to reduce the transport infrastructure demand/supply ratio:
On the supply side, measures can be designed either:
a) to increase the physical capacity of the road system or,
b) to maximize the use of and operational capacity of existing facilities.
The first category includes building additional facilities or physically altering existing facilities to provide additional capacity while the second category includes many familiar traffic management techniques such as those designed:
a) to minimize capacity - reducing factors (for example, turning, parking and loading regulations).
b) to maximize the use of existing road networks (for example, improved traffic signal control).
On the demand side, measures are aimed at managing vehicle use to achieve significant modifications in mode, time, route or destination of vehicle trips. These measures tend to be restrictive and are typically implemented through fiscal or regulatory procedures. Direct control of demand at the micro-level can be executed through measures such as physical restrictions (for example, closing a street) or delay based restrictions (for example, signal control for metering traffic input rates). Queue management does not necessarily fall neatly into any one of the above categories. For instance, queues may be managed in order to make maximum use of existing facilities, or they may be managed such that the input rate of traffic into a sensitive section of the road network is metered (that is, restricted). In other words, a strategy for managing queues in congested traffic operations will be comprised of one or more management techniques and will depend on the network configuration and local demand patterns.
3.2 Traffic Signal Control in Congested Conditions
3.2.1 Introduction
Under congested operations both capacity and operational efficiency are severely degraded, resulting in suboptimal utilization of the available facilities. During "normal" or non-saturated conditions traffic signal control is needed for safety reasons, to minimize delay and number of stops (for efficiency) and to prevent unnecessary congestion. However, during saturated operations, maintaining throughput is essential and strategies are needed to manage in the best way possible.
The now well accepted criteria for optimum cycle length and split at a signal controlled intersection are minimization of delay and of congestion (Webster and Cobbe, (1966)). However, Gordon (1969) recognized that when urban traffic operations are near or above saturation a control scheme is needed for the management of the inevitable queues. He suggests that an intersection control approach should be orientated towards controlling the relative queue lengths on the phases. This approach will then make efficient use of the storage capacity of the streets upstream of the intersection and thereby delay as long as possible the backup of traffic across upstream intersections.
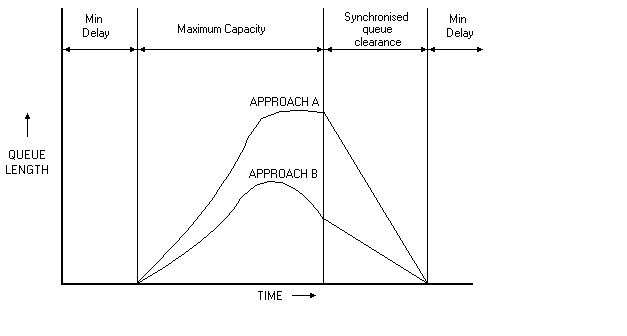
Gazis and Potts (1963) studied the problem of minimizing delay at an oversaturated junction. For fixed-time settings they showed that, when saturation flows in the two critical directions were equal, the minimum delay is given by the settings that cause competing queues to disappear at the same time. They suggest that a minimum delay algorithm should be used during off-peak, changing to a maximum capacity algorithm as soon as the signal becomes saturated (ie the queues on one or more of the approaches consistently fail to clear). At the peak of demand a third algorithm should be introduced to clear queues from the disadvantaged approaches. The aim being to anticipate the fall-off in demand and allocate capacity so that all the queues vanish simultaneously. Finally, the minimum delay algorithm should be reintroduced. The sequence of plan changes is illustrated in figure 1.
The above studies suggest that, in oversaturated conditions, the `objective function' for signal plans should no longer be to minimize delay or some closely related parameter. Instead, the plan should be calculated so as to maximise capacity. Typically this means providing additional green time for the approach or approaches having the greatest saturation flow.

Figure 1. Sequence of traffic signal algorithms for clearance of peak
hour queues.
In a one-way street containing several sets of traffic signals it is usual to provide co-ordination such that traffic passing through one set of signals meets subsequent signals at green. Hence, under relatively free flow conditions, the offset between the start of green for the principal route at successive junctions is determined by the average speed of traffic. In other words the signal plan facilitates a smooth forward progression of vehicle platoons along arterial routes.
As congestion increases and junctions become saturated, queues begin to disrupt movements at upstream junctions. If oversaturation persists for any length of time then the standard fixed-time plans have been found to exacerbate the problems caused by the "spillback" of queues into upstream junctions (May, Montgomery and Quinn, 1988). This means that conventional procedures for optimizing fixed-time signal control, such as TRANSYT (Robertson, 1969), deteriorate rapidly when severe congestion persists and alternative strategies are therefore required to manage queues along the length of an arterial road.
One solution to the spillback problem is manual over-ride of the signals by traffic police at junctions to control such events (for example, Mahalel et al, 1991). This is standard practice in several of the world's most congested cities. An alternative solution is to develop new techniques for signal co-ordination in congested networks. Strategies for minimizing the impact of disruptive queues have been devised by, among others, Pignataro et al. (1978), ITE (1988) and Rathi (1988). A common feature of the strategies is a change in the basic concept of what the offset between signals is supposed to accomplish. Instead of providing for forward progression of vehicle platoons, the signal timings at an upstream junction are determined by the start of green downstream, and the time taken for the front of a queue to move upstream and clear the upstream intersection. Thus, the order of calculation of signal timings is opposite to the flow of congested traffic, so that the term `reverse offsets' is sometimes used. The principle is illustrated in figure 2.
Pignataro et al. (1978) describe a queue management strategy which they term "equity offsets". This strategy, based on the principle of reverse progression, seeks to provide equitable treatment of competing flows at a junction situated upstream of an oversaturated link. They refer to two cases of common interest.
a) Where there are negligible turn-ins from the cross (that is, minor) streets at the upstream junction, the split at the junction can be as commonly determined (eg Webster's delay minimization formula)
b) Where there are substantial turn-ins form the cross streets at the upstream junction, the cross street traffic should be allowed just enough green to put its "fair share" of vehicles into the oversaturated link. If the turn-ins "steal" all the storage space, the through-traffic on the arterial road cannot enter and the oversaturation will propagate rapidly up the arterial.
Pignataro et al.(ibid) do not provide equations to cover all approach width combinations and volume/turn combinations. Instead they set out several principles (listed in Appendix A1) which should be used to govern the formulation of the most appropriate strategy.
There are cases in the literature of empirical studies which have been undertaken to field-test the application of queue management strategies. One example, however is the work of May, Montgomery and Quinn (1988) in Bangkok where procedures were developed to determine fixed-time signal settings capable of managing the queues which form in oversaturated conditions.
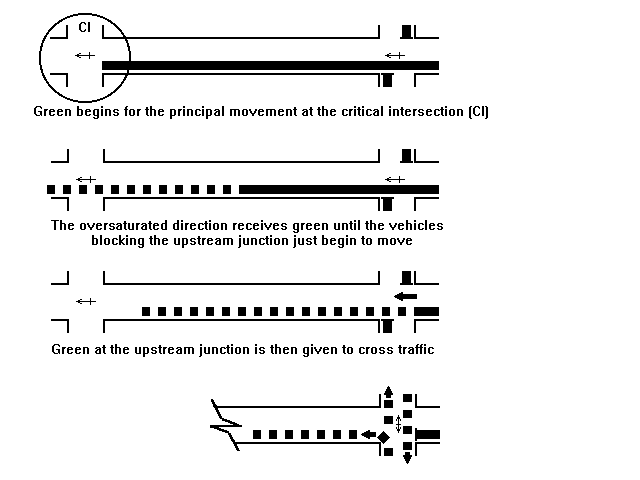
Figure 2. Reverse progression signal offset.
The methods developed in that study involved:
a) predicting the growth and decline of queues from downstream junctions;
b) estimating the speed of the starting and stopping waves which determine (a);
c) identifying the most appropriate time in that stage during which queues should arrive;
d) identifying the most appropriate time in that stage during which queues should be present;
e) adjusting the split between stages to allow for loss of throughput during blocked stages;
f) adjusting the cycle time as necessary in the light of (e).
A number of queue management principles were identified and used to formulate an experimental signal plan for a series of congested junctions in the centre of Bangkok. (These principles are listed in Appendix A2.)
The signal plan was implemented in April/May 1987 and the experiment demonstrated that the queue management strategy performed as planned. Queues arrived in upstream junctions when intended and rarely blocked stage changes. The affected stages were still able to handle the movements which they served. The experimental control was judged successful by local traffic police and traffic engineers and tests showed reduced travel time of around 5% compared with manual police control.
The common feature of most queue management strategies, including the one developed in the Bangkok experiment, is the concept of the "reverse progression" signal offset. The main point of divergence between strategies is, therefore, concerned with the choice of stage (and point of time in the chosen stage) in which to accept a queue from an oversaturated downstream junction. In other words, the various strategies differ in terms of which of the upstream movements affected by spillback are given favourable treatment.
Recent work by May (1991) provides a useful characterisation and generalisation of strategies for the management of queues at upstream junctions. The report discusses a range of options for the stages to be blocked, the timing of arrival of the queue in the blocked stage and the adjustment of split and cycle time. (An extract from this report is reproduced in Appendix A3.)
The various strategy options described by May (ibid) are all based on the assumption that the speed at which the front of the queue moves backwards can be predicted with some degree of accuracy.
Figure 3 is a space-time diagram depicting queue propagation between two junctions. (It is assumed that junction A is oversaturated and that a queue will spillback and block movements at the upstream junction, B). The timing and duration of the queue in junction B will be determined by:-
a) the start of red at A on the approach from B to A, tr
b) the speed of the stopping wave from A to B, ur
c) the start of green at A on the approach from B to A, tg
d) the speed of the starting wave from A to B, ug
e) the length of the link from A to B (strictly from the stopline at A to the junction exit at B, L).
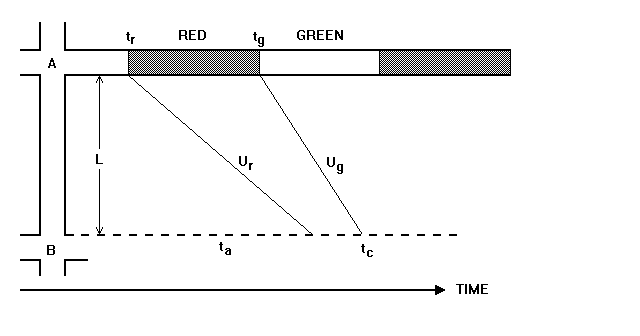
Figure 3. Queue propagation between junctions.
On this basis, the time of arrival of the queue at B, ta, is given by
ta = tr + L/ur (1)
and the time of clearance of the queue at B, tc, is given by
tc = tg + L/ug (2)
The speed of the starting and stopping waves can be determined from observation or calculated by applying the principles of traffic flow theory (see Gerlough and Huber, (1975)). It is interesting to note however, that in the literature as many as three different formulae can be found for predicting the speed of a starting wave. Each formula yields grossly different results and, obviously, only one can be correct. Montgomery and Quinn (1992) discuss and attempt to resolve this problem.
Various queue management techniques can be combined to deal with area-wide congestion on an urban grid network. A demonstration project of this kind has been carried out in the 5th Avenue area of New York (Rathi, (1988)). The network is basically a rectangular grid with Avenues running north-south, and Streets running east-west. The streets function as distributors, carrying traffic to local origins and destinations. The Avenues function primarily as through routes. All the roads are one-way.
It had been found previously that a conventional progression on the N-S Avenues simply did not work. The queues were too long, and furthermore the N-S progressions effectively prevented any coherent E-W progressions along the cross-streets. Sluggish queues on the cross-streets spilled back and blocked movement along the Avenues.
It was calculated that during the morning peak, the optimum offset for most of the Avenue approaches was in fact of the order of one or two seconds. A zero offset was therefore adopted for all the N-S routes. At the same time, capacity considerations dictated that, for the E-W Streets, there should be a negative progression, and the green times should increase progressively from one junction to the next. This resulted in flaring of the green times along the cross streets (see figure 4). A `flared green' progression has the effect of `metering' the number of vehicles released from the upstream signal so that the downstream junction clears. This protects the storage area between junctions, ensures both green periods are fully used and reduces the occurrence of spillback queues. The zero offset and the alternate one-way cross-streets produced an unusual north-south arterial green progression, as depicted in figure 5.
When this control scheme was implemented overall travel time reductions of the order of 20% were obtained, while at the same time morning peak traffic volumes increased by up to 10%. This type of strategy would require further development however, before it could be applied to two-way streets without a critical direction.
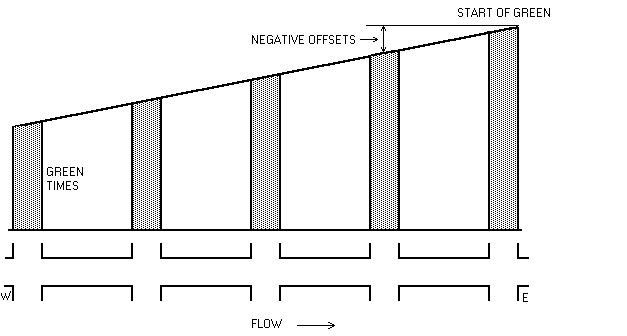
Figure 4. The flared green progression along West-East cross-streets.
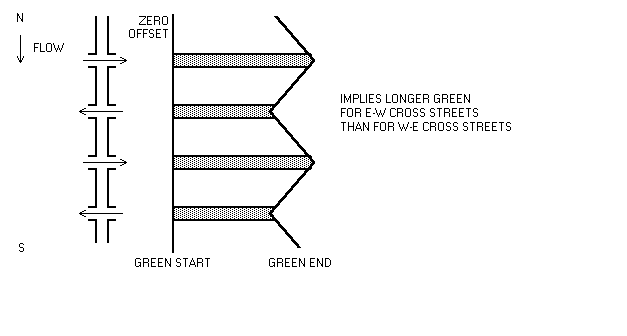
Figure 5. North-South arterial green times.
3.3 Dynamic Change of Algorithm
The techniques described so far were originally designed for fixed time or `static' operation, in which the control algorithm is changed at pre-set times to suit the anticipated traffic demand. If the capacity maximising algorithms are applied too late, queues can quickly build up, leading to catastrophic collapse.
To avoid this situation, it is usual to change the algorithm well before the peak period, causing some unnecessary traffic delay. A better solution might be to install some form of dynamic control system which will trigger a plan change according to the actual traffic conditions at the time.
Dynamic or on-line control systems, which respond to changes in the traffic situation, require a supply of traffic data, usually obtained from loops and/or detectors. There are many ways of treating/using the data and various control algorithms. Shepherd (1992) provides an informative review of dynamic control measures : The review identifies a number of systems operating or under development around the world. The systems described include: PRODYN (France - Henry (1989)); OPAC (USA - Gartner (1989)); SCATS (Australia - Sims and Finlay (1984)); STAUKO/VERON (Germany - Boettger (1971), Boettger (1982) and Boettger (1987)); UTOPIA (Italy - Mauro and Di Taranto (1989) and Mauro et. al. (1984), see APPENDIX A4); and finally SAGE (France - Foraste and Scemama (1987)).
In the UK, the SCOOT (Bretherton, R.D., 1989) control system extends the concept of dynamic control to a whole network of co-ordinated signals. The system is known to work well in conditions of light to medium congestion, but has difficulty dealing with an oversaturated network. If queuing occurs right up to the upstream detector the system cannot detect stationary vehicles and hence "sees" a lower flow (i.e. demand) and reduces the green time, which in turn increases congestion.
The latest release of SCOOT Version 2.4 is described by Bretherton and Bowen (1990). Eleven new features are described in detail, the following were designed to tackle the problem of severe congestion:
3.3.2 Gating and action at a distance
In order to implement "gating", SCOOT must be able to take "action at a distance". That is, it must be able to modify the signal settings at junctions which may be far removed from the area of immediate concern.
The gating logic allows one or more links to be identified as critical, or bottleneck links. A bottleneck link can affect the green time on gated links. The gated links are those links which have been designated to store the queues which would otherwise block the bottleneck link. When the bottleneck link is too busy the green time is reduced on the gated links.
The traffic engineer plays an important role in specifying which links should be bottleneck links and which should be the associated gating links. For a bottleneck link the traffic engineer also specifies the critical degree of saturation above which problems are expected. This critical degree of saturation is used to trigger the gating marker depending on the relative sizes of the current and critical degrees of saturation on the bottleneck link. All of the logic is contained within the split optimiser. When the degree of saturation crosses the critical value from either direction i.e. gating is about to start or end, then two successive stay decisions are imposed to increase the stability of the gating logic.
In congested conditions the offset needs to be set so that capacity is maximised and so that the link is not blocked when the upstream junction is showing green to the critical approach. An offset may be specified to which the optimisers will move the signal settings when congestion is detected on a link. In SCOOT terms, a link is congested when the detector is continuously occupied for at least 4 seconds; the longer the period of continuous occupancy, the higher the level of congestion. Since detectors are normally placed at the upstream end of links, congestion occurs when the link becomes blocked with traffic.
3.3.4 Congestion link facility - information from another link
The latest release of SCOOT makes it possible to specify that a link can use the congestion information from another link either as well as or instead of its own information. Links can be specified as "suppliers" and "receivers" of congestion information, so that the signal timings can be changed accordingly.
It was mentioned earlier (Section 3.2) that the various measures to tackle congestion attempt to reduce the transport infrastructure demand/supply ratio. Discussion has, so far, focused on the supply side of the equation.
On the demand side, measures can be designed to manage and/or control vehicle use to achieve significant modifications in mode, time, route or destinations of trips, and debate on the relative merits of road-pricing and other restraint techniques is gaining momentum. However, in the context of queue management, we are more concerned with measures at the micro-level. Such measures attempt to "meter" or throttle traffic input at a suitable point or points upstream so that demand does not reach the critical level at which flow breakdown takes place. These measures can be applied either locally, to protect a particular junction, or on an area-wide scale. (The `gating' facility in the latest version of SCOOT has already been mentioned.)
Where two traffic signals are sited close together on a busy route, it is common practice to link the controllers and to `flare' the green times. This has the effect of `metering' the number of vehicles released from the upstream signal, so that they can always clear the downstream signal during the same cycle. This protects the storage area between them, and ensures that both green periods are used fully.
Roundabout capacity can be affected adversely by traffic queues within the circulation area, even when the circulating traffic has priority. The capacity can be protected by installing signals on the approaches, a little way upstream of the entry stoplines. The signals `meter' the admission of traffic, and the gaps which they insert into the traffic stream help the roundabout to function more effectively.
The metering technique can, in principle, be extended to cover larger sections of an urban road network. For example, the control scheme developed by Rathi (1988) in New York, (described previously in Section 3.2.3), contains an element of "traffic metering". An important feature of the control policy is the metering effect of the "flared" green times on the cross-streets. At the upstream end, the green times on the cross-streets are relatively short, effectively throttling-back traffic movement at 90 degrees to the area boundary.
In a later paper, Rathi (1991) discusses traffic management control strategies that manage (or meter) the rate of vehicular flow into and within high-traffic density sectors (control areas). He broadly categorizes metering control strategies as:
a) Internal Metering
i) Critical Intersection Control (CIC) to cope with congested conditions that are local in character (that is, queues do not extend into upstream intersections)
ii) Arterial strategies that control the flow along congested arterial roads.
iii) Grid strategies that control the flow along major arterials and along minor cross-streets in a manner that prevents "gridlock" conditions.
b) External Metering
i) Metering traffic along the periphery of a control area to limit the inflow of traffic (while servicing demand at an acceptable level) to improve the overall quality of traffic flow within the control area.
Internal metering is a control strategy applied within a control area whilst external metering limits the traffic volume that can enter the control area. It is argued that the improvement of traffic performance within the control area will more than offset the disadvantages associated with delaying traffic at the periphery. That is, the overall performance of the affected traffic should be improved.
The results of a simulation study by Rathi and Lieberman (1991) indicate that external metering control strategies have the potential to improve traffic operations within and on the approaches to a congested control area. The authors add that the simulation results for their case study suggest that :
"it is virtually essential to apply an external metering policy along the periphery of a control area that is presently congested to the extent that production (vehicle trips serviced) is reduced because of extensive queue spillback."
Some microscopic forms of traffic restraint have been tried successfully in some larger metropolitan areas of developing countries such as Singapore, for example. However, examples of real-world applications of direct measures to control demand on a micro-level (that is, restricting traffic flow on individual approaches or to a small cohesive area) are very limited. One example is the Nottingham Zones and Collar Project (Vincent and Layfield, 1977). The central area of Nottingham was protected by a `collar' which consisted of a ring of traffic signals on the major radial routes. The signal timings were set to produce relatively long queues on the in-bound approaches (bus lanes were provided to allow buses to bypass the queues). Access to the radial routes from residential zones was protected by signals with very low capacity for existing traffic -the resulting queues were intended to deter `rat-running' through the residential zones.
In the event many drivers found ways of reducing or avoiding the extra delays. Some of their techniques such as `red-running' the traffic signals, were illegal. The restraining queues were not as long as they should have been, and they failed to curb traffic demand.
3.4.5 Disadvantages / Objections
The major objections against implementing metering control schemes are that such measures will be unworkable and ineffective and will have an adverse impact on business in the affected area. Another objection is that the restrictions may be unfair to certain groups. Not all metered road users are necessarily contributing to congestion: they may be heading for a route downstream that has spare capacity, or they may be heading for local destinations nearby.
In some cases, the net effect of metering could simply be a transfer of congestion from inside to outside the control area without any change in overall travel time, ambient air quality or other effects of traffic congestion. Furthermore, the concept of metering implies that there will be a temporary accumulation of vehicles at the periphery of the control area, and this raises questions regarding sufficient storage and re-routing of delayed traffic. Finally, it should be borne in mind that, while traffic metering can be applied to protect a busy area from the sudden influx of morning peak traffic, it is less easy to achieve during the evening peak when much of the traffic originates from within the control area.
3.5 Recovery from Severe Congestion
In section 2, the wider objectives for traffic control strategies were identified as being to prevent, to handle and to recover from saturated traffic conditions. Many standard traffic management measures can increase capacity and hence prevent or postpone the onset of congestion. However, once secondary congestion has set in, specific measures are required to cope with it and eventually, to disperse it. Here, the principle of queue management becomes very important and some strategies for handling long queues and spillback problems have been discussed in section 3.2.
In terms of recovering as expeditiously as possible from severe congestion, there appear to be three approaches:
a) to alter the control system to disperse or free critical queues.
b) to provide reserve capacity to relieve congested links.
c) to reduced temporarily the level of demand.
Although in theory long cycles reduce the overall proportion of time lost during phase changes and hence increase overall capacity, in practice the capacity increase is small. A short cycle has the following advantages:
a) it allows a high saturation flow to be maintained throughout the green period (the saturation flow falls if the exit is blocked, which is less likely for short cycles).
b) it is useful for clearing junctions blocked by turning traffic and
c) it provides more frequent opportunities for pedestrians to cross.
Since a reduced cycle time decreases the capacity of the junction as a whole during free flow conditions, it must be allowed to revert to its original value as soon as it has achieved its objective.
3.5.3 Sterilization of Spare Capacity
Sterilizing a proportion of road capacity in a congested area basically means keeping some roads in reserve, perhaps by using variable message signs. Conceivably bus lanes could revert to general traffic use during emergency conditions, not necessarily increasing the capacity, but providing extra storage space for queues thus avoiding spillback conditions.
3.5.4 Driver Information Systems
Dynamic route guidance systems aim not only to direct people to their destination but also to take them on the best route under prevailing conditions. This implies that users will be diverted around incidents and congestion. However, when a jam is detected it may not be possible to transfer traffic to alternative routes without creating a jam elsewhere, possibly causing environmental disturbance on residential roads.
3.6 UTC Operational Strategies
Research on Drive I project V1015 (Gray and Ibbetson, 1991) investigated operational traffic control strategies used by practising traffic engineers for the treatment of recurrent congestion. A survey of operators of nineteen UTC systems in the UK identified a group of ten where operators intervened frequently in local traffic events. Seven of the group used fixed-time plans only, the rest of the group had a mix of SCOOT and fixed-time. The group included; Leeds, Glasgow, Wolverhampton, Coventry, Northants, Lincoln, Liverpool, Sheffield, London and Maidstone.
A list of area strategies was compiled from a literature review and from a pilot study interview at Leeds UTC. Operators at each of the ten cities were asked whether they used any of the strategies in the list (Table 1).
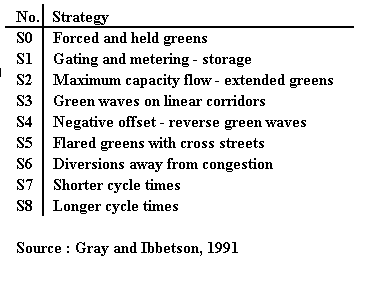
Table 1. List of Area Strategies: From DRIVE I Project V1015.
All of the cities used strategies S1 and S2. Diversion signing (S6) was used in Glasgow and London only. Except where a policy decision had been made to favour pedestrian traffic (Wolverhampton, Sheffield and Liverpool), all other UTCs used S8 to maximize traffic outflow from congested areas. Strategy S0 was used mostly for royal visits or emergency vehicles. Enquiry about strategy S4 (negative offsets) revealed that operators had not used it deliberately, but it emerged as a result of traffic plan adjustments for coping with congestion. S4 was used in Leeds and Liverpool for short-term intervention during very heavy flows.
A follow-up interview survey of operators at Leeds UTC was conducted in March 1992. Operators described several techniques used for coping with recurrent congestion and for handling congestion caused by incidents such as disabled vehicles and accidents. "Metering" was identified as being a valuable tool for limiting the extent of damage (S1) while extended greens (S2) were used to recover from severe congestion. Negative offsets (S4) were recognised as being useful for handling long queues, but such a control strategy was considered difficult to implement unless included in a specific pre-determined plan.
This report has reviewed current techniques used in queue management strategies around the world. It is the techniques themselves that have been most readily identified rather than any set, or sets, of clearly discernible strategies. That is to say, there is a range of techniques which can, and have, been used to manage queues in saturated traffic conditions.
In most cases a combination of various techniques can be used to build up a strategy, or a series of strategies, best suited to the road network configuration and local pattern of demand. The precise form of each strategy will depend on whether the objective is to postpone, to handle, or to recover from highly saturated conditions.
This range of techniques could perhaps be termed a queue management "toolbox". The degree of success of any queue management strategy will then depend upon the traffic engineer's ability to select, combine and use the most appropriate tools in any given situation at any given time.
In the context of a congested urban corridor it seems that a combination of reverse offsets and some form of metering may be most appropriate. The relative balance between these two techniques depends on the prevailing level of congestion and the storage capacity of the approach(es) to the corridor in question.
REFERENCES
Boettger, R. - Siemens - "Koordinierung von Signalanlagen in Stausituationen", (STAUKO) 1987.
Boettger, R. - "On-Line Optimisation of the Offset in Signalised Street Networks" IEE International Conference. Road Traffic Signalling No 207, 1982.
Boettger, R. - Siemens - "Optimal Coordination of Traffic Signals in Street Networks". V International Symposium on the Theory of Traffic Flow and Transportation. University of California, Berkeley, June 1971.
Bretherton, R.D. (1989) SCOOT Urban Traffic control System - Philosophy and Evaluation. IFAC Symposium on Control. Communications in Transportation. September 1989, pp 237-239.
Bretherton, R.D. and Bowen G.T. (1990) Recent Enhancements to SCOOT - SCOOT Version 2.4. 3rd International Conference on Road Traffic Control. IEE Conference Publication 320, pp 95-98.
Foraste and Scemama - INRETS (1987) "An Expert System Approach to Congestion"
Gartner, N.H. (1989) OPAC:Strategy for Demand-Responsive Decentralized Traffic Signal Control. IFAC Control, Computers, Communications in Transportation, Paris, France, 1989, pp 241-244.
Gerlough, D.L. and Huber, M.J. - "Traffic Flow Theory: A Monograph", Special Report 165, Transportation Research Board, National Research Council, Washington DC, 1975.
Gordon, R.L. - "A Technique for Control of Traffic at Critical Intersections", Transportation Science Vol 4, 1969, pp 279-287.
Gray, B.M. and Ibbetson, L. - "Operational Traffic Control Strategy for Congestion", Traffic Engineering and Control, February 1991 pp 60-66.
Henry, J.J. (1989) PRODYN Tests and Future Experiments on ZELT. VNIS `89: Vehicle Navigation and Information Systems, IEEE Conference, Toronto, September 11-13, 1989.
Huddart, K.W. and Wright, C. - "Catastrophic Traffic Congestion and Some Possible Ways of Preventing It". Proc. TRAFFEX International Traffic Engineering Exhibition. Seminar on Congestion, Control and Parking Enforcement. Brighton, April 1989.
Institute of Transportation Engineers - "Management of Damaging Traffic Queues", Technical Committee 4A-24, Washington DC, 1988.
Longley, D. - "A Control Strategy for Congested Computer Controlled Traffic Network", Transportation Research. Vol. 2, 1968, pp 391-408.
Mahalel, D., Yehuda, G. and Shiftan, Y. - "Manual Versus Automatic Operation of Traffic Signals". Transportation Research A. Vol 25A, 1991, pp 121-127.
Mauro, V. and Di Taranto, C. (1989) UTOPIA - CCCT `89 - AFCET Proceedings September 1989 - Paris France.
Mauro, V., Donati, F., Roncolini, G. and Vallauri, M. (1984) A Hierarchial Decentralized Traffic Light Control System, The First Realization. IFAC 9th World Congress, Vol. II, 11G/A-1. 2853-58.
May, A.D., Montgomery, F.O. and Quinn, D.J. - "Control of Congestion in Highly Congested Networks" Proc. CODATU IV Conference, Jakarta, June 1988.
May, A.D. - "Queue Management Project: strategies for the management of queues at upstream junctions". WP346 Institute for Transport Studies, University of Leeds, 1991.
Montgomery, F.O. and Quinn, D.J. - "Queue Management Strategies using Fixed-time Signal Control". 6th International Conference on Road Traffic Monitoring and Control, London, April 1992.
Organization for Economic Cooperation and Development - "Traffic Control in Saturated Conditions", OECD, 1981.
Pignataro, L.J., McShane, W.R., Crowley, K.W. et al - "Traffic Control in Oversaturated Street Networks". National Cooperative Highway Research Program Report 194. Washington DC: TRB, 1978.
Rathi, A.K. - "A Control Scheme for High Density Traffic Sectors". Transportation Research B, 22B (2), 1988 pp 81-101.
Rathi, A.K. and Lieberman, E.B. - "Effectiveness of Traffic Restraint for a congested urban Network: A Simulation Study". Transportation Research Record No 1232. Washington DC: TRB, National Research Council pp 95-102.
Rathi, A.K. - "Traffic Metering: An Effectiveness Study". Transportation Science, July 1991, pp 421-440. 1991.
Robertson, D.I. - "TRANSYT: A Traffic Network Study Tool", Ministry of Transport LR253, TRRL, Crowthorne, 1969.
Shepherd, S.P. - "A Review of Traffic Signal Control" Working Paper 349, Institute for Transport Studies, Leeds, January 1992.
Sims, A.G. and Finlay, A.B. (1984) SCATS. Splits and Offsets Simplified (SOS). ARRB Proceedings Vol. 12, Part 4, 1984.
Vincent, R.A. and Layfield, R.E. - "Nottingham Zones and Collar Study - overall assessment". LR805, Transport and Road Research Laboratory, Crowthorne 1977.
Webster, F.V. and Cobbe, B.M. - Traffic Signals. Road Research Laboratory Technical Paper No 56, 1966, HMSO.
BIBLIOGRAPHY
Al-Madani, H.M.N. - "The prediction of the location of head and tail of queues between two oversaturated signals". Proc 24th UTSG Conference, 1992, Newcastle.
Aymerich, M. and Novo, E. - "Madrid Critical Intersections Antiblocking Strategies". 6th International Conference on Road Traffic Monitoring and Control, London, April 1992.
Clark, S.F. and Montgomery, F.O. - "Queue Management project: calibration of the traffic model". WP347, Institute for Transport Studies, Leeds 1991.
Cremer, M. and Schoof, S. - "On Control Strategies for Urban Traffic Corridors". IFAC Control, Computers, Communications in Transportation, Paris, France, pp 213-219, 1989.
D'Ans, G.C. and Gazis, D.C. - "Optimal Control of Over-Saturated Store-and-Forward Transportation Networks". Transportation Science, 10, 1-19, 1976.
Dunne, M.C. and Potts, R.F. - "Algorithm for Traffic Control". Ops. Res. 12, 1964, pp 878-881.
Gazis, D.C. - "Optimum Control of a System of Oversaturated Intersections". Operations Research No. 12, 1964.
Gazis, D.C. and Potts, R.B. - "The Oversaturated Intersection". In Proc 2nd International Symposium on the Theory of Traffic Flow. London 1963, Paris OECD.
Gerlough, D.L. and Wagner, F.A. - "Improved Criteria for Traffic Signals at Individual Intersections", NCHRP Report 32, 1967.
Green, D.H. - "Control of Oversaturated Intersections". Operational Research Quarterly Vol 18, No 2.
Greenshields, B.D. - "A study of traffic capacity" - Proc. Highways Research Board, Vol 14 HRB, Washington 1934.
Henry, J.J. and Farges, J.L. (1989) Traffic Congestion Control. CCCT `89: Control Computers, Communications in Transportation. 6th IFAC/IFIP/IFORS Symposium on Transportation. Paris, September 19-21, 1989.
Huddart, K.W. and Wright, C. - "Strategies for Urban Traffic Control", The Rees Jeffreys Road Fund "Transport and Society", 1989.
Hunt, P.B., Robertson, D.I., Bretherton, R.D. and Winton, R.I. - "SCOOT - A Traffic Response Method of Co-ordinating Signals", Laboratory Report 1014, Transport and Road Research Laboratory, Crowthorne, Berkshire, 1981.
Lee, B., Crowley, K.W., and Pignataro, L.J. - "Better Use of Signals under Oversaturated Conditions" In better Use of Existing Transportation Facilities, Transportation Research Board Special Report 153. Washington DC: TRB, 1975.
Lieberman, E.B., Rathi, A.K. and King, G.F. - "Congestion Based Control Scheme for Closely Spaced, High Traffic Density Networks", 65th Annual Meeting of the Transportation - Research Board, January 1986.
Lighthill, M.J. and Whitham, G.B. - "On Kinematic Waves: II A Theory of Traffic Flow on Crowded Roads", Proc, Royal Society London, Series A, 1955, 229 (1178).
Longley, D. - "A Simulation Study of a Traffic Network Control Scheme" Transportation Research 5(1), April 1971.
May, A.D. and Montgomery, F.O. - "The Assessment of fixed time signal control in highly congested conditions". Traffic Engineering and Control 27(4) 1989 pp 176-179.
Michalopoulis, P.G. - et al, "An Application of Shockwave Theory to Traffic Signal Control", Transportation Research Record 1194, pp 77-86.
Michalopoulis, P.G. - "Analysis of Traffic Flow at Complex Congested Arterials". Transportation Research Record 1194, pp 77-86.
Michalopoulis, P.G. and Stephanopoulis, G. - "An Algorithm for Real Time Control of Critical Intersection", Traffic Engineering and Control Vol 20, 1979, pp 9-15.
Michalopoulis, P.G. and Stephanopoulis, G. - "Over-Saturated Signal Systems with Queue Length Constraints - I. Single Intersection". Transportation Research, Vol II 1977 pp 413-421.
Michalopoulis, P.G. and Stephanopoulis, G. - "Over-Saturated Signal Systems with Queue Length Constraints - I. Single Intersection". Transportation Research, Vol II 1977 pp 423-428.
Papageorgiou, M., Hadj-Salem, H., Blosseville, J.M. and Bhouri, N. - "Modelling and real-Time Control of Traffic Flow on the Boulevard Peripherique in Paris". IFAC Control, Computers, Communications in Transportation, Paris pp 205-211.
PRIMAVERA: Priority Management for Vehicle Efficiency Environment and Road Safety on Arterials. DRIVE II Project V2016. Commission of the European Communities DGXIII, Telecommunications, Information Industries and Innovation.
Quinn, D.J. - "Calculation of Offsets to avoid Junction Blocking in Oversaturated Conditions". Technical Note 224, Institute for Transport Studies, Leeds.
Quinn, D.J. and Topp, C.F.E. - "Queue management project: testing strategies using the model". WP332, Institute for Transport Studies, Leeds 1991.
Shepherd, S.P. - "Review of Congestion Control", Technical Note 264, Institute for Transport Studies, Leeds-UK, 1990.
Shepherd, S.P. (1991) - "The Development of a Real-Time Control Strategy to Reduce Blocking-Back During Oversaturation using the Microsimulation Model NEMIS". Proceedings 24th ISATA International Symposium on Automative Technology and Automation, Florence, Italy, 20th-24th May 1991, pp 151-158.
Shibata, T. and Yamamoto, T. - "Detection and Control of Congestion in Urban Road Network", Traffic Engineering and Control Vol 25 No 9 1984, pp 438-444.
Stephanopoulos, G., Michalopoulis, P.G., Stephanopoulos, G. - "Modelling and Analysis of Traffic Queue Dynamics at Signalized Intersections". Transportation research A, 13A, 1979 pp 295-307.
Wagner, F.A., Gerlough, D.L. and Barnes, F.C. - "Improved Criteria for Traffic Signal Systems on Urban Arterials". NCHRP Report 73, 1969.
Wagner, F.A., Barnes, F.C. and Gerlough, D.L. - "Improved Criteria for Traffic Signal Systems on Urban Networks". NCHRP Report 124, 1971.
Webster, F.V. - "Traffic Signal Settings". Road Research Laboratory Technical Paper No 39, 1961.
APPENDIX A - QUEUE MANAGEMENT PRINCIPLES
APPENDIX A1 Traffic Control in Oversaturated Street Networks
Pignataro, L.J., McShane, W.R., Crowley, K.W., Lee, B. and Casey, T.W. (1978). "Traffic Control in Oversaturated Street Networks". National Cooperative Highway Research Program Report 194. Washington DC: TRB
Pignataro et al., in Appendix J of NCHRP report 194, suggest that the following principles should be used to determine the signal split at the upstream junction on a congested arterial where a "reverse progression" offset is being operated.
a) The cross-street green should not be so long as to allow turn-ins to take disproportionate amounts of the storage in the oversaturated link.
b) It should be recognized that if the turning demand accumulates, it will interfere with the through movement on the cross street. If possible, storage should be provided.
c) If the turns are indeed significant, and storage and capacity exists, establishment of turn lanes with separate signalization should be considered. In this way, the through movement could be continued.
d) In allowing such cross-street movements, it should be recalled that the through arterial movement needs only as much green as it can effectively use at the critical intersection. Any additional green is, in fact, wasted and is only allocated to the arterial to keep it from the cross turning movement (if signalization by movement does not exist).
e) If necessary, turn prohibitions should be considered so that the cross stream through movement is not severely impacted by queued turning vehicles.
f) If none of the foregoing is feasible refer to the guidelines in Appendix J on the regulation of the spread of (unavoidable) congestion from the upstream intersection.
Note
Recall the assumption that the oversaturation is unavoidable in the one link. And only then is equity off-set implemented. The hierarchy applies to other (cross) links. It does not apply to the original (unavoidably oversaturated) link.
The original link must have unavoidable saturation: neither any signal nor any available nonsignal remedy could have helped it. Only then is this link given up and the best possible done for other traffic.
APPENDIX A2 Control of Congestion in Highly Congested Networks
May, A.D., Montgomery, F.O.M., and Quinn, D.J. (1988). "Control of Congestion in Highly Congested Networks". Proc. CODATU IV Conference, Jakarta, June.
May et al. employed the following queue management principles to control congested urban arterials in Bangkok using fixed-time signal control:
a) Queue length The queue should be as short as possible, given the constraints imposed by optimisation of the downstream junction. For a given number of queued vehicles, queue length is at its shortest when jam concentration occurs; a queue in which a series of starting and stopping waves exist will have a lower concentration and hence a longer length. This suggests that it is preferable for the main flow of vehicles from the upstream junction to join the queue just as the front of it starts to move.
b) Timing of queues If queues are to intrude into the upstream junction, it is essential that they do so during stages of the cycle where they are not disrupting movements which would otherwise not be affected. In particular the queue should not block the junction during the cross street movement or when separate right turn stages are running.
c) Starting and stopping waves Each queue is preceded by a stopping wave and cleared by a starting wave. The times at which these enter the junction are crucial to driver behaviour. A starting wave which arrives at the end of the ahead stage encourages drivers to continue entering the junction in violation of the red signal. In addition, queues which continue in to an upstream junction during a stage change tend to be particularly disruptive. This and consideration (b) suggests that the limits on the appearance of the queue in the upstream junction should be that the stopping wave should arrive after the start of the ahead stage and the starting wave should arrive some seconds before the end of the ahead stage.
d) Adjustment of stage length When a queue is blocking the upstream junction, the affected movement is unable to move and capacity is lost. This extra lost time needs to be accounted for and the stage lengths reoptimised.
e) Adjustment of cycle length Clearly, the shorter the cycle
length the shorter will be the queues on upstream links. That is, provided
that the junction remains undersaturated. It is the high levels of saturation,
together with large turning movements, which necessitate long cycle times.
Once queues occur, the adjustments to stage length in (d) above necessitate
the longer cycle times at upstream junctions. The solution is for these
critical junctions to have double the cycle time of junctions further upstream.
APPENDIX A3 Strategies for the Management of Queues at Upstream Junctions
May, A.D. (1991). "Queue Management Project: strategies for the management of queues at upstream junctions". WP346 Institute for Transport Studies, University of Leeds.
May, sets out a number of principles to govern the control of queues at an individual junction. The principles are based on the assumption that queues from an oversaturated junction will regularly extend and block the next upstream junction. The following is taken from Institute for Transport Studies, Leeds, Working Paper 346 (December 1991):
Appropriate Stages to be Blocked
Earlier work in Bangkok demonstrated clearly that a queue should not exist in a junction during a change of stage. If it does, it is likely to encourage violation of the red signal and aggravate blocking of the junction.
The choice of stage in which to accept a queue from downstream will depend on:
(i) the movements which would as a result be blocked;
(ii) whether these movements are critical (ie. have the highest degree of saturation for the stage) or not and
(iii) the disruption which those movements could cause while blocked.
As general principles:
(a) where possible, queues should be introduced when they only block non-critical movements;
(b) where critical movements have to be blocked, it is generally preferable to block those movements which contribute least to the generation of the queue;
(c) however, it is also preferable to avoid blocking movements which will in turn trap other movements in the junction.
(These principles are discussed in details by May, A.D. (ibid) for the general case of a crossroads between two-way roads.
Timing of the Arrival of the Queue in the Blocked Stage
The main consideration in determining when the queue should arrive during a given stage must be the need to avoid inadvertent blocking during the stage change. This may occur if the queue is timed to arrive early in the stage and the stopping wave arrives earlier than expected. Equally, it may occur if the queue is timed to arrive late in the stage and the starting wave arrives later than expected.
As noted earlier, experience in Bangkok indicated that the speed of the stopping wave was much more variable than that of the starting wave. A sudden surge of input traffic or poor packing in the queue could lead to rapid propagation of the stopping wave, which would thus arrive earlier than expected. Conversely, late arrival of starting waves will only occur when vehicles in the queue fail to maintain saturation flow. Thus generally it is better to allow the queue to arrive as late as possible in the stage, whilst allowing a margin of error for the prediction of starting wave speeds. In the Bangkok experiments this was based on two standard deviations in excess of the expected travel time for the wave from A to B. (Refer to Figure 3 in section 3.2.2 of the main text.)
Such an arrangement is also likely to avoid undue disruption in situations in which saturation flow falls later in the cycle, or where vehicles waiting to make turning movements in the upstream link cause a reduction in saturation flow.
Adjustment of Split and Cycle Time
The process for adjustment of the split between stages is in principle relatively straightforward. The time for which the stage is blocked is first estimated and this is considered as adding to the lost time in the cycle. The remaining time is then allocated optimally between the stages, and the blocked time added to the length of the blocked stage. However, there are several variants of this process which need to be borne in mind.
In some cases blocking can be arranged so that it is not the critical movement in that stage which is blocked. In these situations an initial calculation is required to assess whether the blocked movement, with its movement time reduced by blocking, becomes critical. If it does not, then no adjustment to the split is needed. If it does, then it is necessary to calculate the amount by which that stage would need to be extended to make the blocked movement no more critical than other movements. This is then the equivalent blocked period.
In a limited number of cases more than one queue will arrive at B per cycle. Where this happens two responses are possible. One is straightforwardly to add both blocked periods to the lost time, reoptimise the split and add the blocked periods to the length of the two blocked stages. However, it may be that only one stage is suitable for blocking. In this case it may be possible to double cycle the signal at B, so that its cycle length is half that at A and both queues per cycle at A arrive in the same stage at B. This technique was applied successfully in Bangkok. It does however have implications for capacity at B, as discussed below, and for the performance of junctions further upstream, if they are affected by queues from B.
In certain circumstances, it may be appropriate to modify the stages included in the cycle or their sequence as certain stages in multi-stage cycles may be less affected by blocking. However, care needs to be taken if adding to the number of stages, that the additional lost time does not critically reduce the capacity of that cycle.
The final situation arises where the loss of time from blocking during the cycle renders the cycle over-saturated. It should be noted that shorter cycles are generally to be preferred since they generate shorter queues. However, they also have a higher proportion of lost time. This may be a particular problem with double-cycling, as suggested above. In these situations it will be necessary either:
(i) to reduce the cycle time at A (and other downstream junctions which are generating blocking queues), to reduce queue length or, where this is not feasible on capacity grounds,
(ii) to lengthen the cycle time of upstream junctions.
It will of course be necessary to have a common cycle time throughout,
or common multiples of that cycle time. Where such adjustments result in
the cycle time of A being extended, this will increase the queue length
from A and require further adjustments at B.
APPENDIX A4 Saturation control in the UTOPIA system
The UTOPIA system (Mauro and Di Taranto (1989) and Mauro et al. (1984)), which is actually working on several intersections in Turin, is based on the concept of a fully variable cycle on a rolling horizon.
The local control law, which uses a branch-and-bound technique, performs an optimization over a rolling-horizon of two minutes. Its cost function takes into account, using suitable weighting factors, queue length integrals, private and public vehicle stops, and exceeding of link storage capacity for all incoming links of the intersection. This allows the evaluation of the optimal plan for traffic lights at an isolated intersection. When the local controller is connected in a network, some other factors are included in the cost function.
Each controller receives from its neighbours their traffic lights plan and some other information about downstream links such as queues, storage capacity, forecasts of releases, estimated saturation flow and a reference cycle from the Area Level Control.
Using this information the controller is able to evaluate how its stages planning will affect downstream intersections and how neighbours' cycles will influence its released vehicles.
To coordinate cycles of neighbouring intersections the percentage of released vehicles that will be blocked at downstream intersections is monitored. This, together with the reference cycle, allows the evaluation of the optimum offset between cycles and in low traffic conditions to obtain a green wave in the main direction.
During the branch-and-bound optimization, the controller also evaluates the evolution of downstream queues according to expected releases of the control strategy being considered and penalizes exceeding of the storage capacity. This allows the reduction of the green percentage of the cycle when downstream links are near to saturation conditions.
Modifying and calibrating weighting factors it is possible to obtain a control law that balances the requirement of capacity maximization for low traffic conditions with the requirement of a gating action under saturation or oversaturation conditions while trying to prevent the gating action transferring saturation from the controlled area to its borders.
For a correct evaluation of effects that releases from upstream intersections have on downstream jams, the upstream controller should not consider the number of vehicles in queue, but rather the position of the last vehicle stopped on the downstream link, the so-called horizontal queue.
To avoid saturation and congestion of an upstream intersection it should be realised that the effect on the upstream releases does not change from the time the queue starts to clear until the starting wave reaches the last stopped vehicle on the downstream link.
In this case the optimal relation between start of green stages for upstream and downstream intersections that in low traffic conditions is:
Toff = Tgu - Tgd = Ttr
becomes:
Tgu = Tgd + Ts + Tl - Ttr
where:
Tgu : is start time for green at upstream intersection
Tgd : is start time for green at downstream intersection
Ttr : is the travel time
Ts : is a delay factor that depends on downstream queue at the end of red stage
Tl : is a security time that allows clearance of downstream link
A relation between Ts and downstream queue can be:
Ts = Ns / Vs
where:
Ns : is the number of stopped vehicles at the end of red
Vs : is the starting wave speed into the queue
The Ttr parameter that in low traffic conditions is a constant equal to the travel time between stop lines, in the second formulation becomes a variable that has to consider the smaller space between the stop line of upstream intersection and the end of downstream queue.
To obtain an on-line evaluation of the above mentioned parameters and an automatic calculation of offset an evolution model for horizontal queues is used. In this model we want evolution of horizontal queues to be related to evolution of vertical queues that, at the moment, is available from the Intersection State Observer of each SPOT unit.
If we don't consider arrivals on the queue, the evolution of the vertical and horizontal queue during the green stage follows profiles like the ones shown in Figure A1.
The vertical queue (V [veh]) stays constant for a time equivalent to the reaction time of drivers (Tl [s]) and then decreases, to a first approximation, with a slope equal to the saturation flow of the link (s [veh/s]).
The horizontal queue (H [m]) stays constant until the starting wave reaches the last stopped car (Ts [s]) and then decreases with a slope equal to the average cruise speed (vc [m/s]).
Common points of the two models are that we can consider that both clear at the same time (Tc [s]) and at the start of the green stage, as during red stages, they are linked by the average length of a vehicle (lveh):
H(0) = V(0)*lveh
If we consider as status variables of the vertical queue at time t0 the amplitude of the queue (V(t0)) and the passed green time (Tg(t0)), and for the horizontal queue the amplitude (H(t0)) and the time when the queue starts to clear (Ts(t0)) it is possible to evaluate the status of a queue by knowledge of the other one.
If we assume that t=0 at the beginning of the green then Tg=t0 and:
Ts(t0) = t0*(1-s*lveh/vc) + V(t0)*(1/s-lveh/vc) + Tl*s*lveh/vc
H(t0) = H(0) = V(t0)*lveh + s*lveh*(t0-Tl) if Ts>t0
H(t0) = H(0) - vc*(t0-Ts) if Ts<=t0
These relations are always valid during the clearance of the queue and also takes account of arrivals on both queues until time t0.
The control strategy requires that controllers receive from their neighbours the actual status of downstream vertical queues, "translate" it to the status of the horizontal queue and then, while evaluating different strategies in the branch and bound, propagate the status of horizontal queue according to the model:
Ts(t0+) = Ts(t0) + A(t0+)*(1/s-lveh/vc)
H(t0+) = H(t0) + A(t0+)*lveh if Ts>t0+
H(t0+) = H(t0) + A(t0+)*lveh - vc*(t0+-Ts) if Ts<=t0+
where A(t0+) is the sum of arrivals on the queue from time t0 to to+ and depends on releases expected for the strategy being examined.
When the horizontal queue becomes greater than the maximum queue a non-linear weighting factor penalizes the excess. In this way, stage planning that provides releases while the downstream queue is really clearing or even is little are favourite.
In the case of a link that has more than one green stage where different turnings are allowed, the saturation flow is no longer a constant but varies with the stages.
The Observer module of each local unit provides an estimation of saturation flow for each set of turnings that "see" the green in the same stage, so it is possible to evaluate and send to upstream controllers the percentage of the total saturation flow that is released in each stage.
These will use this percentage to modify the above mentioned s parameter according to downstream stages.
A control strategy similar to that described above but using the vertical queue model has been tested in a laboratory environment using the NEMIS traffic micro-simulator and has given good results, while the horizontal queue model is being implemented and will be tested within the PRIMAVERA project both in a laboratory environment and then on a test site.
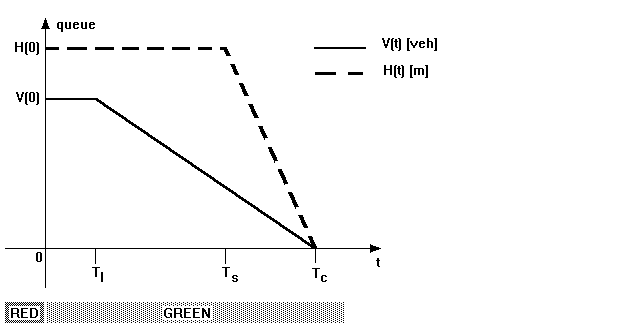
Figure A1. Horizontal and vertical queue evolution.