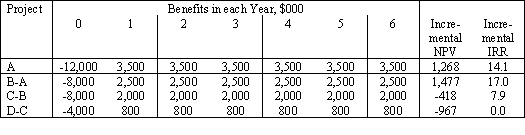When and How to Use NPV, IRR
and Adjusted IRR
Part of Toolkit for the Economic Evaluation of World Bank Transport Projects
(Institute for Transport Studies, University of Leeds, 2003)
The abbreviations stand for:
- Net Present Value (NPV)
- Internal Rate of Return (IRR)[*]
- Adjusted Internal Rate of Return (AIRR)
1 Background to NPV, IRR and Adjusted IRR
All three are summary measures of project performance. Each one provides a single figure summarising the impact of the project on economic welfare. Each of the three measures does, however, give subtly different information:
- NPV focuses on the total welfare gain over the whole life of the project;
- IRR and Adjusted IRR focus on the rate at which benefits are realised following an initial transport investment[†]. Table 1 gives an illustrative example of some results.
Table 1: Example Results - Highway Rehabilitation Project
|
Economic
analysis over 30 years: NPV@12%
per
annum = $530m IRR = 20%
per annum Adjusted IRR = 15% per annum |
As we will see below, these results would indicate that the project met the World Bank’s basic acceptability criterion. They also provide a basis for comparison with other uses of the resources. First, though, we consider the meaning and calculation of the NPV, IRR and Adjusted IRR.
|
Net Present Value = = where Bt are the benefits in year t, Ct are the costs in year t, r is the discount rate, and n is the horizon year.
Note that if Present Value
of Benefits (PVB) is the sum of the discounted benefit stream, and Present Value of Costs
(PVC) is the sum of the discounted cost stream, then NPV = PVB – PVC. An example is given in Table 2. The NPV can be calculated using spreadsheet software such as Microsoft Excel, most of which conveniently have an NPV function built-in. Caution
Excel users: Users should exercise caution, since Excel starts discounting from the first year of the series. In an appraisal for the World Bank, the first year will often be the Base Year (the year in which t = 0 and the discount factor is 1.0). Under these circumstances, take care to calculate the NPV from year t = 1 onwards and add the undiscounted net benefit in year t = 0 to the result. Note also that if costs are being calculated for each calendar year, benefits must be calculated for the same period. Care should be taken when inputting benefits from HDM-4 to ensure that the time periods are consistent. |
Net Present Value
NPV is a measure of the absolute welfare gain over the whole life of the project[‡]. Future benefits and costs are discounted at a compound rate, r, typically 12% per annum[§]. Benefits, net of costs, are then summed across all years. Box 1 shows how the calculations are made.
Internal Rate of Return
IRR is the rate at which benefits are realised following an initial transport investment. It can be thought of as the constant compound rate of return which is equivalent to the actual – fluctuating – rate of return over the project lifetime.
IRR is also closely related to the NPV: the IRR is the rate of discount at which the NPV of the project is reduced to zero.
Box 2: Calculating the IRR
|
This can be solved by a search procedure, which is
available in most spreadsheet packages - such as Microsoft Excel. An example is given in Table 2. |
Table 2: Example Calculations - Highway Rehabilitation Project
|
|
Adjusted Internal Rate of Return
The Adjusted IRR is useful because it provides a test of the robustness of the IRR to one of the underlying assumptions – an assumption which is not always valid. The IRR assumes that all the benefits from the project can be re-invested at the rate of teh IRR, yielding further benefits in the next period. However, the benefits from transport projects – for example, in the form of travel time savings – may not be re-investible. If they are not, or they are reinvestible but at a lower rate, then the IRR will overstate the true rate of return, and the Adjusted IRR will give an estimate of the true value.
Box 3: Calculating the Adjusted IRR
|
The Adjusted IRR can be
calculated using the MIRR function in Microsoft Excel. The Reinvest Rate should be entered in the form R%. Excel will then calculate the Adjusted IRR. |
In the example given in Table 2, if the benefits cannot be re-invested at all, the Adjusted IRR will be 8%. If the benefits can only be invested at a market interest rate of 12% rather than at the IRR, the Adjusted IRR will be 15%. Again, the calculations can be made using spreadsheet software. In practice, it might be reasonable to assume simply that:
- the revenue stream is fully reinvestible;
- the user benefits are not reinvestible, or reinvestible only at a lower rate.
2 When and how should each measure be used?
A Net Present Value or an Internal Rate of Return is an essential result from any economic appraisal, including appraisals of transport projects. The Handbook on Economic Analysis of Investment Operations (World Bank, 1998) [1] is a source of general advice on the usage of NPV and IRR.
The appropriate use of NPV and IRR (or Adjusted IRR) depends on the decision context. Four important types of decision are worth highlighting.
(i) The accept/reject decision. The World Bank considers a project to be acceptable if it reaches the following minimum standard of performance [**]:
|
Criteria for acceptability: NPV > 0 or IRR > the discount rate, r |
This test will be applied to all projects, however, it is only the first of several hurdles to be jumped.
(ii) Choosing between mutually exclusive alternatives. Economic appraisal is also used to inform the choice between alternative courses of action. In transport, these choices include:
- choice between different routes for road and rail links, and different locations for ports and interchanges of all types;
- choice between different engineering solutions, eg. tunnels versus bridges, or metro versus light rail solutions;
- choice between different approaches to improving transport, eg. infrastructure investment versus improved maintenance (see Note Treatment of Maintenance [Link] versus organisational reform (see Note Economic Appraisal of Regulatory Reform [Link] versus pricing options (see Note Evaluation Implications of Sub-Optimum Pricing [Link]);
- choice between public provision, private provision and partnership arrangements; and
- choice of projects to include within a Programme or Plan for transport.
Here the question is not simply whether the project would contribute to economic welfare, but whether is it has been shown to be the best of the available alternatives in these terms. This can be tested by comparing projects in terms of their NPV and IRR, as follows.
When all the alternatives being compared are investment projects, featuring an initial investment followed by a flow of benefits in the future, one (or preferably both) of the following summary measures should be provided: - NPV for both projects A and B - Incremental IRR of Project A over Project B, IRRA-B (for calculations see Box 4) When the alternatives being compared do not fit the standard investment profile, the appropriate comparison is: - NPV for both projects A and B |
To start with, there is a presumption in favour of the solution with the lowest capital cost. This can be designated Project A. Alternatives to Project A can be compared with Project A either based on their NPV – a higher NPV is preferred – or by undertaking an incremental analysis, as follows.
Box 4: Incremental Analysis
|
|
Incremental analysis applies where the choice is between one solution or another. There may of course be situations where both projects could usefully be undertaken. If so, the relevant criterion is the total NPV of the set of investments proposed.
In practice, projects are often composed of packages of components. In this case, incremental analysis should be used to test whether particular components are worthwhile, in terms of their incremental NPV or IRR.
(iii) Timing of investment. The timing of a project is an important decision that needs to be analyzed in every case. Just because a project’s benefits exceeds its costs it does not mean that the project should be started immediately. Postponing a project may change the time profile of benefits and costs and hence the project’s NPV. If the profile of benefits and costs is not changed, but only postponed, then timing is not an issue, as the present value of the benefits and costs will change proportionally by the discount factor used. Thus, if (a) the present value of a project’s benefits discounted at 20 percent is $12M, (b) the present value of costs is $6M, and (c) postponing the project one year merely shifts all costs and benefits by one year, the present value of both benefits and costs will be reduced by the same percentage, as will the NPV of the project itself. In these cases, the sooner the project starts, the higher the NPV.
If, on the other hand, the benefit or cost profile changes with postponement, then timing becomes an issue. Consider a project that begins to generate benefits during its third year of life, two years after its initiation (Table 3 – top panel). The project has a four year operating life.
Table 3: Postponement of Project
|
Year |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Benefits, $M |
0.0 |
0.0 |
2.0 |
7.0 |
7.0 |
8.0 |
0.0 |
|
Costs, $M |
-3.0 |
-2.0 |
-1.0 |
-1.0 |
-1.0 |
-1.0 |
0.0 |
|
Net Benefits, $M |
-3.0 |
-2.0 |
1.0 |
6.0 |
6.0 |
7.0 |
0.0 |
|
...after postponement: |
|
|
|
|
|
|
|
|
Benefits, $M |
0.0 |
0.0 |
0.0 |
7.0 |
7.0 |
8.0 |
8.0 |
|
Costs, $M |
0.0 |
-3.0 |
-2.0 |
-1.0 |
-1.0 |
-1.0 |
-1.0 |
|
Net Benefits, $M |
0.0 |
-3.0 |
-2.0 |
6.0 |
6.0 |
7.0 |
7.0 |
The net present value of this flow, discounted at 12%, is $8.1M. If we were to postpone the project by one year and thereby shift all benefits and costs one year into the future, the net benefits as well would be shifted by one year and hence their present value would be reduced in proportion to the discount rate and the project’s net present value would fall to 7.2 = 8.9 ÷ 1.12. In this case waiting would not pay.
Suppose, however, that a one year postponement were to shift all costs by one year, leaving the gross benefits unchanged. The new net benefits profile would be as shown in the bottom panel of Table 3. By postponing the project we would be forgoing $2M of gross benefits in year two in exchange for $8M of gross benefits in year six. The net present value of this new flow, discounted at 12 percent, would be $11.3M, indicating that postponement would be advisable. The difference between these two examples is that in the first case postponement merely shifted the cost and benefit streams by one year, while in the second case postponement altered the streams. The optimal timing for a project occurs in the year in which its NPV peaks. The best way to identify that year is to examine the effects of postponement year by year until the optimal year is found. It should be noted that in both cases we evaluated the NPV of the project with respect to the same base year, namely year zero, when t = 0. In all cases we need to evaluate the present value of the flows with respect to the same base year.
3 The role of the discount rate
It is clear that a key variable when calculating the NPV, IRR and Adjusted IRR is the discount rate.
|
The World Bank convention is to use a discount
rate of 12 percent when evaluating Bank–financed transport projects. This figure is not
necessarily a precise reflection of the opportunity cost of capital in
borrower countries, instead it can be viewed as a rationing device for World
Bank funds. If appraisal requirements at the country level call for a different discount rate, then the 12% rate and the country-specific rate may both be tested. The results using the 12% rate should be reported in the Project Appraisal Report and will be important in the World Bank’s decision-making. Bear in mind that the discount rate is one of the easiest appraisal parameters to vary – particularly once a spreadsheet has been set up to make the calculations. |
A strong justification is required if a discount rate other than 12% is to be used as the main rate. A discount rate lower than 10% is unlikely to be justified, since most research has shown that the cost of capital for developing countries is higher than 10%. Task managers will need to demonstrate that any alternative rate has been justified in the Country Assistance Strategy. Further advice and further reading references on discounting are given in the earlier section on Net Present Value.
4 Summary
Summary measures of project performance, such as the NPV, IRR or AIRR, are used to indicate the overall performance of a project under economic evaluation:
- either an NPV or an IRR (or AIRR) is an essential result, to be included in the Project Appraisal Report;
- as a minimum, to be ‘acceptable’ a project should have an NPV greater than zero or an IRR (or AIRR) greater than the discount rate, which is conventionally 12% for Bank-funded transport projects;
- the NPV or IRR (or AIRR) measure should also be used to compare alternative solutions, for example alternative routes for road and rail links, and different locations for ports and interchanges of all types;
- The World Bank has a presumption in favour of the solution with the lowest capital cost – incremental analysis can then be used to assess the value for money offered by more expensive alternatives;
- sometimes it can pay, in economic terms, to postpone the implementation of a project to a later date – the NPV can be used to test whether the timing of investment is optimal.
5 Further Reading
[1] The World Bank (1998), Handbook on Economic Analysis of Investment Operations. Washington, DC: The World Bank. Technical Appendix. Available online at:
http://www.worldbank.org/education/economicsed/project/projwork/Handbook.pdf